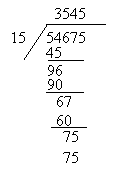
Oleh:
SAFINAZ BT. M. ANNUAR, NELLIE GAN HONG
SUAN & OON BOEY LAY
ABSTRAK
Kajian ini mengenal pasti jenis kesilapan
penyelesaian masalah yang dilakukan oleh murid-murid di dua buah sekolah
iaitu SRJK(T) Batu Caves, Selangor dan SRB St Henry Slabi, Serian Sarawak.
Dua persoalan yang dikaji adalah (a) apakah jenis kesilapan yang sering
dibuat oleh murid dalam penyelesaian masalah bahagi dan (b) apakah perbezaan
kesilapan di antara murid sekolah bandar dan luar bandar. Instrumen untuk
mengumpul data terdiri daripada 2 ujian diagnostik melibatkan
kemahiran operasi bahagi Tahun 5. Ujian Diagnostik I terdiri daripada 10
soalan berbentuk lazim dan Ujian Diagnostik II terdiri
daripada 5 soalan berbentuk penyelesaian masalah. Kajian ini mencungkil
beberapa jenis kesilapan dan salah konsep yang sepunya
di kalangan kedua-dua kumpulan. Cadangan untuk mengatasi kesilapan-kesilapan
ini juga disertakan.
PENGENALAN
Latar Belakang Kajian
Sukatan Pelajaran
KBSR Matematik menekankan pelajar menguasai kemahiran yang melibatkan operasi-operasi
+, -, x, ¸ . Operasi-operasi itu merupakan asas kepada menguasai
kemahiran-kemahiran lain dalam matematik. Menurut laporan Taraf Pencapaian
Di kalangan Murid-murid Tahun 2 dan Tahun 6 (Yap 1982), pencapaian mereka
dalam matematik hanya 37.5%. Ini menunjukkan satu fenomena yang kurang
memuaskan berkaitan kira mengira di kalangan murid. Berdasarkan laporan
tersebut kajian ini telah meninjau kelemahan dan kesilapan murid dalam
menangani penyelesaian masalah yang melibatkan operasi bahagi.
Kajian di sekolah bandar telah dilaksanakan oleh peserta Kursus Diploma
Perguruan Khas 1997/98. Ini mencetuskan keinginan membandingkan pencapaian
penguasaan kemahiran menyelesaikan masalah bahagi dengan murid sekolah
luar bandar.
Objektif Kajian
Kajian ini bertujuan untuk :
i. mengenal pasti jenis kesilapan dalam penyelasaian masalah
bahagi murid tahun 5.
ii. mengenal pasti sama ada terdapat perbezaan jenis kesilapan antara
murid-murid sekolah bandar dan luar bandar.
Persoalan Kajian
Apakah jenis kesilapan yang sering
dibuat oleh murid dalam penyelesaian masalah bahagi?
Apakah perbezaan jenis kesilapan
antara murid sekolah bandar dan luar bandar?
Bidang Kajian
Kajian ini mengenal pasti tahap pencapaian
murid Tahun 5 terhadap penyelesaian masalah bahagi.
Responden terdiri daripada 42 orang murid
Tahun 5 di sekolah bandar SRJK(T) Batu Caves, 68100 Batu Caves, Selangor.
Sekolah luar bandar pula ialah SRB St Henry Slabi 94700 Serian,
Sarawak, yang melibatkan 32 orang murid Tahun 5.
Limitasi Kajian
Kajian hanya tertumpu pada 2 buah
sekolah sahaja dengan melibatkan murid-murid Tahun 5 seramai 42 orang dari
SRJK(T) Batu Caves,Selangor dan 32 orang dari SRB St Henry Slabi Serian
Sarawak. Hasil kajian ini tidak menyeluruh kepada semua murid Tahun
5 di sekolah-sekolah lain. Dua buah sekolah ini juga terpilih kerana
guru-guru yang membantu mentadbirkan ujian diagnostik itu pernah berkursus
di maktab di mana pengkaji kajian bertugas.
Kepentingan Kajian
Kajian ini menjelaskan jenis kesilapan
yang dilakukan oleh murid dan mengenal pasti tahap pencapaian mereka
dalam penyelesaian masalah bahagi. Hasil kajian ini akan dapat memberi
sumbangan kepada para pendidik dan perancang kurikulum
berhubung masalah pengajaran dan pembelajaran penyelesaian masalah dan
cara-cara mengatasinya.
Definisi istilah
Dalam kajian ini “penyelesaian masalah
bahagi” bermaksud kemahiran melakukan operasi bahagi dan kemahiran
mengenal pasti operasi bahagi yang diperlukan untuk menyelesaikan
masalah harian.
TINJAUAN LITERATUR
Beberapa kajian yang telah dijalankan oleh ahli psikologi, pakar matematik dan guru matematik menunjukkan ada pelbagai sebab murid melakukan kesilapan dalam pengiraan bahagi.
Sesuatu kemahiran yang hendak diajar kepada murid perlulah diterangkan konsep disebaliknya.
Menurut Fehr dan Phillips (1977) pembelajaran formal operasi bahagi menjadi lebih bermakna apabila bahasa yang betul dan konsep yang betul diperkenalkan serentak. Contoh-contoh yang sesuai boleh dibuat bersama murid. Umpamanya 5 kumpulan 4 orang murid dan 2 orang terasing, apabila dikumpulkan bersama menjadi 22. Mungkin juga murid-murid mengira begini iaitu dua dua , tiga tiga , lima lima, dengan pelbagai objek seperti kerusi, meja dan buku membuat murid mengingat tentang bahagiannya (perkongsian/pengagihan) dalam pembelajaran yang formal tentang aspek-aspek bahagi.
Kesediaan murid mempelajari cara-cara menyelesaikan masalah yang melibatkan operasi bahagi tertakluk kepada tahap pencapaian atau penguasaan mereka mempelajari tentang operasi tambah, tolak dan darab. Swenson (1973) berpendapat kemahiran membahagi tidak digunakan sekerap kemahiran tambah, tolak dan darab serta diperkenalkan lewat maka kurang peluang untuk kemahiran membahagi diamalkan. Inilah menyebabkan murid menghadapi kesulitan menyelesaikan masalah bahagi.
Menguasai fakta asas congak darab dan bahagi merupakan aspek penting dalam menguasai kemahiran menyelesaikan masalah yang melibatkan operasi bahagi. Menurut Ruslia (1990) dalam kajiannya di Sekolah Kebangsaan Tasik, Ipoh, Perak; antara punca masalah dalam kelambatan dan kelemahan mencongak pengiraan melibatkan operasi bahagi adalah sikap murid itu sendiri.
Manakala Ramly (1992) berpendapat murid tidak ada inisiatif untuk menghafal sifir atau fakta asas bahagi. Antara kelemahan murid menyelesaikan masalah bahagi adalah murid tidak tahu cara membina ayat matematik bagi operasi bahagi, tidak ada asas membaca dan kurang yakin terhadap kebolehan diri serta sikap malu untuk bertanya.
Kesimpulan yang agak sama telah dikesan
dalam kajian Mazniah (1994) tentang kelemahan murid dalam penyelesaian
masalah bahagi. Masalah-masalah yang dihadapi murid adalah menulis ayat
matematik yang terbalik pembahagi dan yang dibahagi, tidak dapat membaca
dan memahami maksud atau kehendak soalan serta ragu-ragu tentang maksud
yang dikemukakan secara lisan dan tidak dapat menulisnya kepada bentuk
ayat matematik.
METODOLOGI KAJIAN
Instrumen Kajian
Instrumen untuk mengumpul maklumat terdiri
daripada 2 ujian diagnostik. Ujian Diagnostik I terdiri daripada
10 soalan berbentuk lazim dan Ujian Diagnostik II terdiri daripada 5 soalan
berbentuk penyelesaian masalah. Soalan-soalan dalam kedua-dua ujian
diagnostik melibatkan kemahiran operasi bahagi Tahun 5 iaitu:
| 1. | membahagi sebarang nombor kurang daripada 100,000 dengan sebarang nombor satu digit dengan mengumpul semula berbaki dan tanpa baki. |
| 2. | membahagi sebarang nombor kurang daripada 100,000 dengan sebarang nombor dua digit dengan mengumpul semula berbaki dan tanpa baki. |
| 3. | menyelesaikan masalah bahagi yang melibatkan sebarang nombor yang kurang daripada 100,000 dengan sebarang nombor satu digit dengan mengumpul semula berbaki dan tanpa baki. |
| 4. | menyelesaikan masalah bahagi yang melibatkan sebarang nombor yang kurang daripada 100,000 dengan sebarang nombor dua digit dengan mengumpul semula berbaki dan tanpa baki. |
Populasi dan Pensampelan
Populasi kajian ini terdiri daripada murid-murid
Tahun 5 dari dua buah sekolah iaitu 42 orang murid SRJK(T) Batu Caves Selangor
dan 32 orang murid SRB St Henry Slabi Serian, Sarawak. Daripada jumlah
74 orang murid itu 32 orang murid lelaki dan 42 orang adalah murid
perempuan.
Prosedur Kajian
Guru sekolah berkenaan mentadbir ujian diagnostik I dan II kepada murid dalam dua waktu pengajaran matematik. Jawapan murid disemak oleh guru itu. Dalam Ujian Diagnostik I murid yang melakukan kesilapan dalam jawapanya dikehendaki membuat pembetulan di depan guru, manakala bagi Ujian Dignostik II apabila terdapat kesilapan, guru yang sama akan mengemukakan beberapa soalan sambil murid membuat pembetulan.
Soalan-soalan yang dikemukan adalah :
1. Bolehkah anda baca soalan itu dengan
kuat?
2. Apakah yang dikehendaki oleh soalan
itu?
3. Apakah maklumat yang diberi dalam soalan
itu?
4. Apakah operasi yang hendak digunakan
untuk menyelesaikan soalan itu?
5. Sekarang bolehkah anda cuba gunakan
operasi itu untuk menyelesaikan soalan?
6. Betulkah jalan kerja yang anda lakukan?
7. Kenapa berlaku kesilapan?
Adakah tadi anda lupa caranya?
Kajian di SRJK(T) Batu Caves telah dijalankan
pada April 1998 oleh peserta Kursus Diploma Perguruan Khas 1997/98 Maktab
Perguruan Teknik, manakala pengumpulan data bagi SRB St Henry Slabi dibuat
oleh guru sekolah itu sendiri pada April 1999. Guru itu juga adalah bekas
pelajar Maktab Perguruan Raja Melewar bagi Kursus Sijil Perguruan Khas
1993. Beliau juga berminat mengetahui pencapaian muridnya dalam kemahiran
bahagi.
ANALISIS DATA
Pengenalan
Bahagian ini membentangkan data-data yang diperoleh daripada ujian-ujian diagnostik yang dijalankan. Data yang terkumpul seterusnya dianalisis.
Punca-punca Kesilapan
Ada beberapa punca yang menyebabkan berlakunya kesilapan di kalangan responden. Pengkaji mengenal pasti punca kesilapan seperti :
1. Tidak berhati-hati atau cuai. Membaca
soalan dengan cepat dan sekali imbas sahaja.
2. Tidak menulis sifar di tempat yang
sepatutnya atau mengelakkan / tertinggal menulis sifar.
3. Tidak menguasai nilai tempat sa, puluh,
ratus, ribu, dan puluh ribu serta tidak menulis nombor mengikut sa, puluh,
ratus, ribu, dan puluh ribu
Kes-kes ganjil di mana
a) simbol tambah disertakan
b) menulis titik perpuluhan dan titik
di sebalik sifar
c) mendarab untuk mendapatkan jawapan
d) tidak tahu sifir
5. Tidak membaca soalan dengan berhati-hati
(malas membaca cerita yang melibatkan nombor lebih daripada satu digit).
Tidak berhati-hati atau cuai
Keadaan ini wujud di dalam semua kes, baik
dalam kes murid yang cerdik mahu pun yang lemah . Ia terjadi kerana murid
terlalu gopoh untuk menghabiskan soalan hingga melakukan kecuaian ketika
memberi jawapan. Ada juga yang terlalu yakin dengan jawapan yang mereka
beri hingga tidak menyemak jawapan sebelum menghantar kertas soalan.
Murid membuat kesilapan disebabkan
kecuaian. Apabila murid ini ditanya mengapa berlaku kesilapan,
mereka menyatakan bahawa, mereka berlumba-lumba hendak menghabiskan
soalan secepat mungkin.
Murid cuai dalam menulis satu angka maka
jawapan menjadi salah.
Contoh:
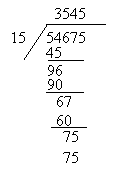
Kebanyakan murid mengaku mereka terlalu
ghairah untuk menghabiskan soalan sehingga terlalu asyik menulis jawapan
dan tidak peduli untuk menyemak jawapan.
Tidak menulis sifar di tempat yang sepatutnya atau tertinggal sifar
Tidak menulis sifar boleh dikategorikan kepada dua kesilapan iaitu terhindar daripada menulis sifar kerana dianggap tidak bernilai atau tidak diperlukan.
Contoh:
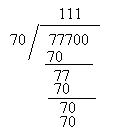
Murid mengaku tertinggal sifar dan ada pula mengatakan sifar itu tiada nilai.
Tidak menguasai nilai tempat sa, puluh,
ribu, dan puluh ribu dan tidak menulis nilai tempat sa, puluh, ratus, ribu,dan
puluh ribu
Ramai murid yang membuat kesalahan ini
ragu-ragu tentang nilai tempat. Walaupun mereka tahu jawapan yang betul
tetapi oleh kerana kurang arif tentang nilai tempat, mereka menulis pada
nilai tempat yang salah. Ada juga di antara mereka mengganggap bahawa mereka
boleh menulis di sebarangan bahagian nilai tempat asalkan jawapan
itu betul.
Contoh:
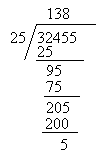
Kes-kes ganjil
Kes-kes ganjil ini dibahagikan kepada 4 jenis. Pengkaji telah mendapati murid-murid menambah, mendarab dan meletak titik perpuluhan di tempat-tempat tertentu dan kesilapan yang wujud disebabkan oleh murid yang tidak tahu sifir.
Contoh ( i )
Murid menambah untuk mendapatkan jawapan

Contoh ( ii )
Murid mendarab untuk mendapatkan jawapan
:
9363 ÷ 3
Contoh (iii)
Murid meletakkan titik perpuluhan di tempat
– tempat tertentu.
9363 ÷ 3 = 31.21
Contoh (iv)
Murid tidak dapat membahagi kerana lemah
atau tidak tahu sifir. Murid belum lagi lancar dengan sifir maka membahagi
nombor dengan hanya meletakkan sebarang nombor sebagai jawapan.
Tidak membaca soalan
Murid didapati tidak membaca soalan
dengan berhati-hati. Ada juga responden tidak suka membaca soalan panjang
atau merasa terlalu sukar hendak faham soalan panjang. Segolongan responden
tidak tahu membaca dan menghadapi masalah membaca walau pun perkataan yang
tidak melibatkan matematik.
Apabila dibandingkan % kesilapan (rujuk
Jadual Jenis Kesilapan) bagi setiap jenis kesilapan kedua-dua sekolah,
didapati kesilapan murid tertumpu kepada jenis kesilapan cuai dan
tidak membaca soalan dengan teliti. Sebilangan kecil murid SRJK(T) Batu
Caves melakukan kesilapan disebabkan menganggap sifar tidak mempunyai nilai.
Ada juga murid yang agak tidak menguasai kemahiran operasi bahagi dalam
kes-kes ganjil menunjukkan langkah-langkah pengiraan yang luar biasa iaitu
menambah, mendarab dan meletakkan titik perpuluhan di tempat-tempat tertentu
dalam jawapan. Kes ganjil tidak terdapat pada murid-murid SRB ST Henry
Slabi, tetapi kebanyakan mereka melakukan kesilapan sebab tidak tahu sifir.
Manakala segelintir murid SRJK(T) Batu
Caves belum menguasai nilai tempat bagi nombor.
RUMUSAN DAN CADANGAN
Memandangkan jenis kesilapan yang kerap
dilakukan oleh murid terdiri daripada tiga punca iaitu cuai, tidak tahu
sifir dan tidak membaca dengan lebih teliti; berikut adalah beberapa cadangan
bagi mengatasinya.
1. Guru perlu memastikan murid menguasai
kemahiran seperti nilai tempat sa, puluh, ratus, ribu, puluh ribu
serta menulis nombor mengikut nilai tempat dan sifir darab. Murid mesti
cekap dalam operasi darab dan cekap menggunakan sifir darab. Murid boleh
diminta melafazkan sifir darab tertentu sebelum permulaan kelas bagi mengingat
kembali sifir itu. Membanyakkan latihan darab juga dapat membantu ke arah
ini.
2. Lebih tumpuan harus diberi kepada operasi
bahagi yang asas dengan nombor ringkas. Pada peringkat awal
pengenalan operasi bahagi fakta asas bahagi ini hendaklah ditekankan.
3. Menyemak jawapan dijadikan amalan murid.
Selepas selesai mengira semakan jawapan boleh dibuat iaitu mendarab jawapan
dengan pembahagi.
24 ÷ 3 = 8
Guru jelaskan apabila didarab jawapan
dengan pembahagi akan menghasilkan yang dibahagi. Secara ringkasnya
Semak: Jawapan x pembahagi = yang
dibahagi
8 x
3 =
24
25 ÷ 3 = 8 baki 1
Guru mengingatkan murid apabila ada baki,
langkah pertama adalah mendarab jawapan dengan pembahagi. Kemudian
langkah kedua pula menambahkan baki kepada jawapan dalam langkah
pertama
8 x 3 = 24
24 + 1 = 25
Secara ringkasnya
Semak: jawapan x pembahagi
+ baki = yang dibahagi
8
x 3
+ 1 = 25
Secara tidak langsung, murid mendapat
latihan pengiraan yang melibatkan operasi bercampur.
4. Sentiasa merujuk kepada sifir
ketika mengajar operasi bahagi
1 x 7
= 7
2 x 7
= 14
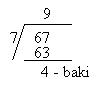
9 x 7 = 63
5. Membuat anggaran jawapan
digalakan. Sebagai contoh (Rujuk soalan 2 Ujian Diagnostik II), murid boleh
dengan mudah mengira wang yang diterima oleh 10 orang iaitu RM 910.80 .
Anggarkan wang yang diterima oleh 12 orang ( bilangan orang lebih 2 daripada
10 ) amaun yang kurang sedikit daripada RM910.80 iaitu antara RM700 –RM800.
Kirakan amaun/jumlah yang sebenar diterima dan bandingkan dengan amaun
yang dianggarkan tadi.
6. Guru perlu kemukakan pelbagai masalah
yang melibatkan operasi bahagi dan juga operasi
bercampur . Ini dapat mengelakkan murid mengeluarkan nombor-nombor terlibat
dan melakukan operasi bahagi tanpa membaca soalan. Apabila operasi bercampur
terlibat, murid perlu membaca dengan teliti bagi mempastikan langkah pengiraan
serta operasi yang terlibat.
RUJUKAN
Atan Long, Pelbagai Kaedah Mengajar,
Fajar Bakti Sdn. Bhd. Kuala Lumpur, 1991
Esther J. Swenson, Teaching Mathematics
to Children, Macmillan Co.,New York, 1973
Frank J. Swetz & Liew Su Tim, Pengajaran
Matematik KBSR, Fajar Bakti Sdn. Bhd..Kuala Lumpur, 1988
Howard F. Fehr & Jo McKeeby Phillips,
Teaching Modern Mathematics in the ElementarySchool, Admission
Wesley Publishing Co.,
1977
Liou Hou Sin, Teori dan Strategi Pengajaran
Matematik Rendah, Jurnal: Kementerian Pendidikan Malaysia,
Keluaran 69, Disember
1986
Mazniah bt. Abu Bakar, Kelemahan Murid-murid
dalam Penyelesaian Masalah Operasi Bahagi, Sekolah Kebangsaan
Batang Kali,Hulu Selangor,
Guru Pakar Matematik, 1994
Soon Sang & Siew Fook Cheong, Pengajaran
& pembelajaran Matematik untuk Pengajaran Sekolah
Rendah, Heinemann(Malaysia)
Sdn. Bhd., 1986
Michael L. Mahaffey & Alex F. Perrodin,
Teaching Elementary School Mathematics, F.E. Peacock Publishers, Illinois,
1973
Ramly b Hanif, Kelemahan Murid dalam Menyelesaikan
Masalah Operasi Bahagi Tahun 4 Sekolah Perak
Kebangsaan Tuallang
Sekah, Gopeng, Kursus Sijil Perguruan Khas, 1992
Ruslia bt Nordin, Kelemahan Murid Tahap
II Menguasai Fakta Asas Congak Operasi Darab dan Bahagi, Sekolah
Kebangsaan Tasek Ipoh,
Perak, 1990